
Puno ime ovog italijanskog matematičara je Leonardo Pisano Fibonači poznat i kao Leonardo iz Pize. Bio je sin Guilielmo i član familije Bonači. Fibonači je ponekad sebe nazivao imenom Bigollo, što znaci dobar za ništa (ljenjivac) ili putnik. Fibonači je rođen u Italiji, ali se obrazovao u Sjevernoj Africi, gdje je njegov otac bio angažovan u diplomaciji i predstavljao trgovačke poslove republike Pisa. Živjeli su u Bužiju, mediteranskom gradu na obalama Kabilije u sjeverozapadnom Alžiru. Grad leži na ušću Wadi Soummam blizu Mount Gouraya i Cape Carbona. Fibonači je podučavao matematiku u Bužiju i dosta putovao sa svojim ocem te tako prepoznao ogromne prednosti decimalnog brojnog sisetma koji se tad u svakodnevnom životu koristio u islamskim zemljama. Fibonači piše u svojoj poznatoj knjizi "Liber abaci" :
"Kada me je otac, koji je bio postavljen kao javni bilježnik na carini u Bužiju radeći za Pisan trgovine, pozvao sebi dok sam još kao dijete imao oštro oko za korisne stvari, želio je da ostanem živjeti s njim i steknem znanje u školi računanja. Zatim, kad sam se upoznao sa umjetnošću indijskih devet simbola znanje o umjetnosti mi je godilo iznad svega drugog i došao sam razumjeti je bez obzira na način na koji se ista u svim svojim različitim formama studirala u Egiptu, Siriji, Grčkoj, Siciliji i Provansi."Fibonači je završio svoja putovanja oko 1200 godine i u to vrijeme se vratio u Pisu. Tu je napisao brojene važne tekstove koji su igrali bitnu ulogu u oživljavanju drevnih matematičkih vještina i u tome je njegov veliki doprinos. Fibonači je zivio u doba prije nego se pojavila gutenbergova štamparska mašina, tako da su njegove knjige rukom pisane i jedini način da postoji kopija njegove knjige je da postoji već jedna knjiga predhodno rukom napisana. Od ovih knjiga do danas su sačuvane "Liber abaci" (1202), "Practica geometriae" (1220), "Flos" (1225), i "Liber quadratorum". Zahvaljujući ovim nekoliko rukom pisanih kopija sretni smo što danas imamo pristup radu ovog matematičara. Zna se, međutim, da su napisani i neki drugi tekstovi, koji su nažalosti izgubljeni. Njegova knjiga o komercijalnoj aritmetici "Di minor guisa je" izgubljena kao i njegov komentar o desetoj knjizi Euclid-ovih Elemenata sa brojnim raspravama o iracionalnim brojevima koje je Euclid razmatrao sa geometrijskog aspekta. Postoji mišljenje da se Fibonačijev rad u vrijeme kada je Evropa bila poprilično nezainteresovana za obrazovanje uveliko ignorisao. Ova konstatacija ipak ne stoji jer je upravo veliki interes za njegov rad bez sumnje jako doprinio njegovoj važnosti i popularnosti. Fibonači je bio savremenik Jordanusa, ali istovremeno i sofisticiraniji matematičar čija su dostignuća bila jasno prepoznata, iako su ga uglavnom praktične primjene, prije nego apstraktne teoreme, učinile poznatijim od njegovih savremenika.
U to vrijeme rimski imperator je bio Frederick II. Proglašen je kraljem Njemačke 1212 i onda krunisan kao sveti rimski imperator od strane pape u crkvi svetog Petra u Rimu novembra 1220-te godine. Frederick II je štitio grad Pisu koji je bio u sukobu sa Genoaom na moru i sa Lucca i Florencom na kopnu. Kontrola države se vršila kroz trgovinu i industrijske izrađevine. Frederik je u ove svrhe osnovao Univerzitet u Napulju 1224 godine. On je postao svjestan važnosti Fibonačijevog rada preko učenika na svom dvoru koji su održavali redovan kontakt sa Fibonačijem još od njegovog povratka u Pisu 1200-te godine. Neki od ovih učenika su Michael Scotus, astrolog na dvoru, Theodorus Physicus, filozof i Dominicus Hispanus koji je sugerisao Frederick-u da se upozna sa Fibonačijem. Johannes od Palerma, drugi član dvora Fredderick-a drugog, postavio je brojne probleme kao izazove pred matematičara Fibonačija. Tri problema Fibonači je riješio a rješenja postavio u radu "Flos" i poslao Frederick-u II. Navest ćemo par detalja vezano za ove matematičke probleme. Poslije 1228 godine postoji samo jedan poznat dokument koji se odnosi na Fibonačija. To je odluku koju je izdala Republika Pisa 1240 u kojoj se plata dodjeljuje: "...ozbiljnom i učenom učitelju Leonardo Bigollo..." Ova plata je data Fibonačiju, jer je prepoznat značaj njegovog doprinosa, u davanju savjeta oko računanja i poduke građana, kojim je zadužio grad. "Liber abaci", objavljen 1202 godine, nakon Fibonačijevog povratka u Italiju, je posvećen Scotusu. Knjiga razmatra aritmetiku i algebru koje je Fibonači skupio tokom putovanja islamskim svijetom. Knjiga, koja je u velikom broju kopirana i imitirana, prezentuje indijsko-arapski decimalni brojni sistem, ovo je prvi korak uvođenja arapskih brojeva u Evropu. Premda je glavni dio knjige o korištenju arapskih brojeva, poznatih kao arapski brojni sistem, uzastopne linearne jednačine su takođe predmet u ovog rada. Mnogi od problema koje je Fibonači razmatrao u "Liber abaci" su slične onim koji su prethodno obrađivani u arapskim izvorima. Drugi dio knjige "Liber abaci" sadrži veliku kolekciju problema iz trgovanja. Oni se odnose na cijene robe, kako izračunati profit u transakcijama, kako pretvarati različite valute koje su se koristile u mediteranskim zemljama, i problemi koji su nastajali u Kini. U trećem dijelu su predstavljeni fibonačijevi brojevi i fibonačijev niz po kojima je ovaj matematičar danas poznat: "Neki ćovjek stavi par zećeva na mjesto okruženo sa svih strana zidovima. Koliko parova zećeva će nastati nakon godinu dana, ako se predpostavlja da svaki mjesec svaki par rodi novi par koji nakon drugog mjeseca postaje zreo za produkciju?"
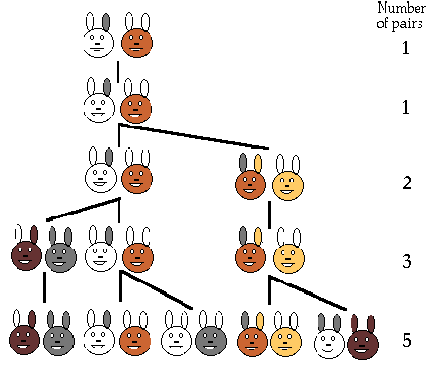
Rezultujući niz je 1,1,2,3,5,8,13,21,34,55, ... Ovaj niz u kojem je svaki broj suma predhodna dva broja, se pokazao veoma korisnim i javlja se u mnogo različitih područja matematike i nauke. Fibonacci Quarterly je moderna novina posvećena studiranju matematike koja se odnosi na ovaj niz. U drugom dijelu su dati i problemi tipa: "...Pauk se penje određen broj stopa uz zid svaki dan i oklizne se nazad stalan broj puta svaku noć, koliko dana mu je potrebno da se popne na zid....Lovaćki pas čija se brzina povećava aritmetički goni zeca čija se brzina takodje povecava aritmetički, koliko će se rastojanje preći prije nego pas ulovi zeca ?..." Razmatrani su i problemi savršenih brojeva, problemi koji uključuju teoremu Kineskog ostatka i problemi o sumiranju aritmetičkih i geometrijskih nizova. Fibonači brojeve kao što je korijen iz 10 sa racionalnim aproksimacijama i sa geometrijskim konstrukcijama obrađuje u četvrtom dijelu knjige. Drugo izdanje knjige "Liber abaci" Fibonači je napisao 1228 godine. Fibonačijeva knjiga, "Practica geometriae" je napisna 1220 i posvećena je gore već pomenutom Dominicusu Hispanusu. Knjiga sadrži veliku kolekciju geometrijskih problema raspoređenih u osam poglavlja sa teoremama iz euklidovih knjiga. Pored geometriskih teorema sa preciznim dokazima knjiga uključuje i praktične primjere kao što je izračunavanje visine visokih objekata putem metode sličnih trouglova. Zadnje poglavlje predstavlja ono što sam Fibonači zove geometrijskim vještinama. U knjizi "Flos" Fibonači daje preciznu aproksimaciju rješenja jednačine 10x+2x2+x3=20. Ovo je bio jedan od problema koji je pokušao riješiti Johannes od Palerma. Ovaj problem nije postavio Johannes od Palerma već ga je preuzeo iz knjige o algebri od Omara Khayyama gdje je to riješeno pomoću presjeka krugova i hiperbola. Fibonači dokazuje da korijen (nepoznata) jednačine nije ni cio broj ni razlomak, niti kvadratni korijen razlomka. On zatim nastavlja: "I zato što nije moguće riješiti ovu jednačinu ni na jedan od načina gore navedenih ja sam nastojao da dođem do približnog rješenja."Bez objašnjavanja svojih metoda Fibonači daje apriksimativno rješenje u seksadecimalnoj notaciji (brojni sistem po bazi 60) kao 1.22.7.42.33.4.40. Pretvorano u decimalni broj ovo iznosi 1,3688081075 što je tačno do devete decimale i predstavlja nevjerovatno postignuće. "Liber quadratorum", napisan 1225 godine, je Fibonačijev najimpresivniji rad iako to nije rad po kojem je poznat. Naziv knjige znači knjiga o kvadratima i razmatra oblast teorije brojeva. Fibonači je zabilježio da se kvadratni brojevi mogu konstruisti kao suma neparnih brojeva koristeći formulu n2+(2n+1)= (n+1)2. Fibonači je dokazao mnogo teorija iz oblasti teorije brojeva kao što je: "...ne postoje x i y takvi da su x2+y2 i x2-y2 istovremeno kvadrati... x4-y4 ne može biti kvadrat..." On je definisao koncept "congruum"-a, to je broj oblika ab(a+b)(a-b). Fibonači je dokazao da congruum mora biti djeljiv sa 24 i takođe je pokazao da za x i c ako su x2+c i x2-c kvadrati, vrijedi da je c congruum. Takodje je dokazao da kvadrat na može biti congruum. Knjiga "Liber quadratorum" Fibonačija postavlja kao matematičara koji je dao glavni doprinos teoriji brojeva u vremenu od Diophantusa do francuskog matematičara Pierre de Fermata u 17-tom vijeku.


