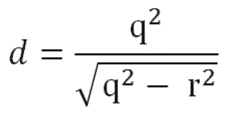Arapski matematičari su bili zainteresovani za razne konstrukcije na sfernoj površi. Problem određivanja prečnika kugle upotrebom isključivo šestara i lenjira je riješio Tabit ibn Kura (836 - 901).
Zadatak je forumlisan na sljedeći način: "Koristeći Euklidova oruđa (lenjir i šestar) naći prečnik date materijalne lopte."
U nastavku pročitaj na koji način je problem u svoje vrijeme riješio ovaj poznati arapski matematičar.
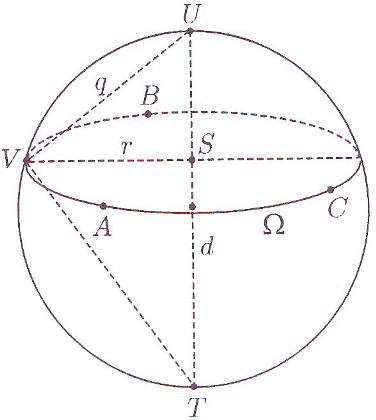
Konstruišimo pravougli trougao ΔUVT koji za visinu ima poluprečnik r, a za hipotenuzu prečnik d = |UT| (vidi sliku). Dužina q stranice UV ovog pravouglog trougla može se izmjeriti šestarom - to je isti otvor šestara korišten pri crtanju kruga Ω u prvom koraku. Znajući q i r, iz pravouglog trougla ΔUVT pomoću proporcije nalazimo:
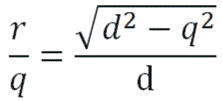
Slijedi da je prečnik materijalne lopte: