Kvadratura kruga je jedan od najstarijih i najpoznatijih matematičkih problema:

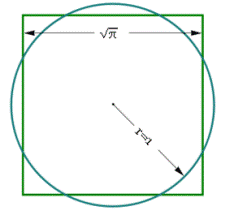
Konstruisati kvadrat

čija je površina jednaka

površini datog kruga.

Prečnik kruga treba umanjiti za devetinu i na taj način se dobije stranica traženog kvadrata.

Grci se nisu zadovoljili sa približnim rješenjima. Prve sačuvane bilješke o problemu kvadrature kruga svjedoče da se njime bavio i Anaksagora (5. vijek p.n.e.), osnivač atinske filozofske škole. Antifon iz Atine (5. vijek p.n.e.) je izračunao površinu kruga tako što je upisivao u njega sve veće pravilne ntougle. Vjerovao je da će na taj način pomoću lenjira i šestara naći tačnu vrijednost.

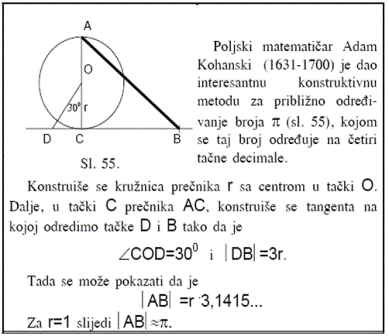
Arhimed je u Mjerenju kruga dokazao da je obim kruga tri puta veći od prečnika, i još nešto više, naime za manje od sedmine, ali za više od deset sedamdesetjednina. Na taj način Arhimed dolazi do vrijednosti:

π=3,14.

Mnogo kasnije njemački matematičar Lindman (1882) će pokazati da je broj π nemoguće elementarno konstruisati. Takođe, dokazao je da π nije rješenje nijedne algebarske jednačine s cjelobrojnim
koeficijentima. Problem kvadrature kruga se praktično svodio na konstrukciju broja π.