Koristeći jednostavne geometrijske argumente čuveni antički matematičar Heron iz Aleksandrije (oko 65 - oko 125) je posmatrao sljedeći problem.
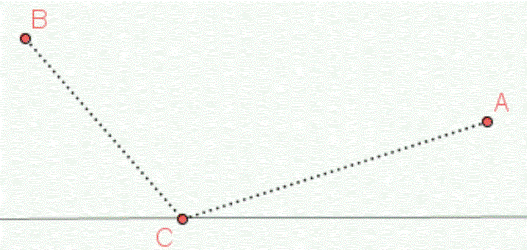
A i B su dvije date tačke sa iste strane prave. Odrediti tačku C na pravoj tako da suma rastojanja od A do C i od C do B bude minimalna.
U praktičnom životu možemo reći da je prava željeznička pruga, dok su tačke A i B gradovi, a tačka C je buduća željeznička stanica koju treba sagraditi. Potrebno je odrediti mjesto gdje će se graditi željeznička stanica tako da je ukupna dužina puteva kojima su gradovi spojeni sa stanicom najkraća.
Geometrijsko rješenje Heronovog problema se jednostavno izvodi pomoću slike ispod.
[file w=650 h=450]/java/osmi/heronovo_rastojanje.html[/file]
Neka je A' tačka simetrična tački A u odnosu na pravu i neka je C proizvoljna tačka na pravoj. Spojimo B sa A' i označimo sa C0 tačku presjeka duži BA' i prave. kako je trougao Δ CAA' jednakokraki to imamo
|BC| + |CA| = |BC| + |CA'|
Zbog toga je
|BC| + |CA| = |BC| + |CA'| ≥ |BA'| = |BC0| + |C0A|
gje jednakost važi samo ako se tačka C poklapa sa C0.
Posljednja relacija je rješenje Heronovog problema. Tražena tačka koja obezbjeđuje minimalnu sumu rastojanja je presjek date prave i duži čiji su krajevi tačke B i A' simetrična datoj tački A u odnosu na pravu 


