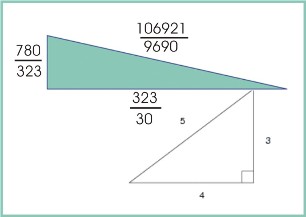
Tim od pet matematičara su dobili dosad najveći skup kongruentnih brojeva (.pdf dokument) rješavajući trilion drevnih matematičkih problema koji se tiču površina pravouglih trouglova. Prvi problem kongruentnih brojeva postavio je perzijski matematičar Al Karađi još u desetom vijeku.

      Iznenađujuće težak problem uključuje određivanje cijelih brojeva koji mogu biti površina pravouglih trouglova čije su stranice takođe cijeli brojevi ili razlomci. Površina ovakvog trougla se zove kongruentni broj. Tipičan primjer  je poznati pravougli trouao tipa "3-4-5" čije su stranice cijeli brojevi a površina je 6, tako da je 6 kongruentni broj. Najmanji kongruentni broj je 5 što je površina pravouglog trougla čije su stranice
,
i
.


      Tim je koristio napredne tehnike množenja i pohranjivanja velikih brojeva. "Teži dio posla je bio kreirati opštu bazu kompjuterskog koda koja dovoljno brzo može obavljati ovaj tip proračuna," rekao je Bill Hart (Univerzitet Warwick)."Kad smo ovo učinili samo pisanje kompjuterskog programa nije iziskivalo dosta vremena."

      Hart i Gonzalo Tornaria (Universidad de la Republica in Uruguay) su za ovaj zadatak koristili Selmer kompjuter na Warwick univerzitetu, dok su Mark Watkins (Sydney univerzitet), David Harwey (New York univerzitet) i Robert Bradshaw (Washington univerzitet u Seattle-u) koristili Sage kompjuter na Washington univerzitetu.

      "Smisao i motiv rješavanja starih problema ovog tipa često nije potpuno jasan. Treba imati na umu da njihovo rješavanje generira dosta interesantnih i korisnih istraživanja tako što matematičari razvijaju nove načine i pristupe rješavanja", rekao je Brian Conrey, direktor Američkog instituta za matematiku.

      "Prije nekoliko godina kombinovali smo ideje iz teorije brojeva i fizike da predvidimo statistiku ponašanja kongruentnih brojeva. Bilo mi je veoma drago vidjeti da su naša predviđanja bila prilično tačna", rekao je matematičar Michael Rubinstein (Univerzitet Waterloo).


     Rad nosi naziv "Kongruentni brojevi theta koeficijenta do 10¹²" (.pdf dokument).

Izvor: Američki institut za matematiku, 22. Septembar 2009; ScienceNow, 23. Septembar 2009.