Puno ime Šaraf al Din al Tusija je Šaraf al Din al Muzaffar ibn Muhammad ibn al Muzaffar al Tusi. O njegovom životu se zna veoma malo, ali se nekoliko detalja može rekonstruisati iz referanci koje se pojavljuju u radovima drugih naučnika tadašnjeg doba. Iz imena se da zaključiti da je rođen u regiji Tus, na sjeveroistoku Irana. Ova regija je uključivala grad Tus i obližnji grad Meshed, visoko u dolini rijeke Kashaf. Ono što je sigurno je da je veći dio života proveo u različitim gradovima. Godine 1154, Seljučki Turci osvajaju Damask u Siriji i čine ga glavnim gradom njihove velike imperije. Grad je napredovao, što je mnoge i privuklo, uključujuči i al Tusija. Oko 1165 godine al Tusi je bio u Damasku, gdje ga je Abu`l Fadl podučavao radovima Euclida i Ptolomeja. Abu`l Fadl je bio interesantna osoba, on je radio kao drvosjeća, stolar prije nego što je al Tusija podučavao matematici. Iz Damaska je al Tusi prešao u Aleppo, drugi najveći grad u Siriji.
U Aleppo-u, al Tusi je podučavao najmanje tri godine, i interesantno je da je podučavao kao važan član jevrejske zajednice u tom gradu; teme koje je podučavao su bile nauka o brojevima, astronomske tablice i astrologija. Iz Aleppo-a, al Tusi je otišao u Mosul, grad na sjeverozapadu Iraka. U to vrijeme gradom je vladala dinastija Zingid, a sam grad je bio politički centar. U Mosulu al Tusi je podučavao najpoznatijeg učenika Kemal al Din ibn Yunus-a, a kasnije i Nasir al Din al Tusija, najpoznatijeg islamskog naučnika u to vrijeme. Da je al Tusi stekao reputaciju izvrsnog učitelja matematike govori podatak da je veliki broj učenika dolazio iz udaljenih gradova kako bi bili njegovi studenti.
Al Tusi je vjerovatno boravio u Mosul kad je Saladin prebacio svoje snage iz Sirije i započeo sa ujedinjenjem područja Sirije, Mezopotamije, Palestine i Egipta. Saladin je osvoji Damask 1174 godine i otprilike u to vrijeme al Tusi je napustio Mosul i vratio se u Iran. U Bagdadu je podučavao do kraja svoga života i za to vrijeme je napisao svoj najpoznatiji rad iz algebre opisan u nastavku.
Postoje brojni al Tusijevi radovi koji su bili važni za razvoj matematike. Najvažniji je opisao Sorton kao:
...studij o algebri... (napisana) 1209 je poznata kroz komentar nepoznatog autora.
Sarton koristi rijec „komentar“ sto je malo obmanjujuće, budući da nepoznati autor u rukopisu piše:
U ovom radu želim da sumiram umjetnost algebre , i prilagodim ono što je preživjelo od velikog filozofa Šaraf al Din al Muzaffar ibn Muzaffar ibn Muhammad al Tusija, i smanjim njegovo prekomjerno izlaganje na modernu veličinu; eliminisao sam njegove tabele koje je koristio pri računanju i riješavanju problema.
Šta je u al Tusijevom radu Studija o jednačinama? U osnovi to je studija o kubnim jedančinama, ali koja ne prati al Karađijevu školu algebre. Prije će biti kako Rashed piše:
...da predstavlja osnovni doprinos nekoj drugoj algebri čija je namjena proučavanje krivih pomoću jednačina, što vodi ka početku algebarske geometrije.
U studiji, kubne jednačine su podjeljene u 25 različitih vrsta. Prvo je al Tusi diskutovao dvanaest vrsta kvadratnih jednačina. Zatim je pogledao osam vrsta kubnih jedančina koje uvijek imaju pozitivno rješenje, a onda pet vrsta koje možda nemaju pozitivno riješenje.
Metod koji je al Tusi koristio je prilično izvanredan. Za ilustraciju navest ćemo kako al Tusi ispituje pod kojim uslovima jednačina x3+a=bx ima riješenja, gdje su a i b pozitivni brojevi. Naravno ovdje se koristi moderno obilježavanje, dok je al Tusi svojevremeno, u matematici, koristio riječi. Al Tusi prvo komentariše da ako je t rješenje ove jednačine onda je t3+a=bt i budući da je a>0, t3 <bt, onda je t<√b .
Dalje al Tusi bilježi da je bx- x 3=a i nalazi maksimum funkije y= bx- x3. Koristeći derivaciju ovog izraza, al Tusi nalazi maksimum u tački ![]() i zamjenom nazad u jednačini y= bx- x3 nalazi maksimalnu vrijednost za y =
i zamjenom nazad u jednačini y= bx- x3 nalazi maksimalnu vrijednost za y = ![]() . Dakle jednačina bx- x3 =a ima rješenje za
. Dakle jednačina bx- x3 =a ima rješenje za ![]()
Zatim al Tusi utvrđuje da jednačina ima pozitivan korijen ako je
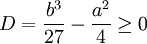
gdje je D diskriminanta jednačine.
Al Tusijev analitički pristup jednačinama označava nastanak algebarske geometrije - proučavanje krivih korištenjem jednačina, a u riješavanju nemogućih jednačina uveo je nove ideje i metode i otvorio više pravaca matematičkih istraživanja. Nekoliko novih ideja, koje se obično pripisuju kasnijim evropskim matematičarima, pripadaju al Tusiju.
On je prvi put u historiji sistematski izložio pojam maksimuma algebarskih izraza, koji se često pogrešno pripisuje francuskom matematičaru Fransoa Vijetu (1540-1603) - odrediti vrijednost nepoznate veličine x za koju kubna funkcija te nepoznate dostiže maksimum. Da bi to uradio al Tusi je izračunao vrijednost promjenljive veličine x za koju je izvod gornje funkcije jednak nuli. Al-Tusi nije za izvod koristio arapsku riječ istog značenja, ali je na sasvim jasan način dao lokalnu analizu, studiju maksimuma i uveo pojam izvoda- što je bilo od ključnog značaja za razvoj algebarske geometrije
Zatim al Tusi daje ono što danas nazivamo Ruffini-Horner metodom za određivanje približne vrijednosti korijena kubne jednačine. Iako su ovu metodu koristili raniji arapski matematičari za nalaženje približnih vrijednosti za n-ti korijen cijelog broja, al Tusi je prvi koji je primijenio metod za rješavanje generalne jednačine ovog tipa.
Drugi poznati al Tusijev rad je onaj u kojem opisuje linearni astrolab, ponekad nazvan i „Al Tusijev štap“, koji je njegov izum. Kao instrumenti za mjerenje položaja zvijezda astrolabi su bili nezamjenjivi na pomorskim putovanjima u vrijeme velikih evropskih otkrića.


