Ovog matematičara često zovu i "otac algebre " a puno ime mu je Abu Džafer Muhammed ibn Musa Al Khwarizmi. O njegovom životu iz perioda rane mladosti, kao ni tačan datum rođenja i smrti, ne zna se mnogo. Nažalost, zbog nedostatka ovog saznanja dolazi se u iskušenje da se prave pretpostavke bazirane na veoma malo dokaza. Toomer sugeriše da ime Khwarizmi govori da je porijeklom iz područja južno od Arala u centralnoj Aziji. Prije nego razmotrimo neke od stvarnih činjenica o njegovom životu ukratko ćemo sagledati kulturni i naučni ambijent u kojem je Khwarizmi radio.
Harun al-Rashid je postao peti halifa abasidske dinastije 14 septembra 786 godine, otprilike u vrijeme kada je Khwarizmi i rođen. Harun je vladao, iz svog dvora u glavnom gradu Bagdadu, islamskom imperijom koja se prostirala od Mediterana pa sve do Indije. On je svoj dvor oplemenio kulturnim događajima i pokušao uspostaviti intelektualne discipline koje u to vrijeme nisu bile razvijene u arapskom svijetu.
Imao je dva sina, starijeg al-Amin i mlađeg al-Mamun. Harun je umro 809-te godine, a al Mamun ga je naslijedio i iz Bagdada nastavio vladati islamskim carstvom. Nastavio na sličan način na koji je to započeo njegov otac i osnovao akademiju nazvanu Kuća Mudrosti gdje su prevođeni grčki naučni i filozofski radovi. Takođe je izgradio i biblioteku rukopisa, prvu veliku biblioteku koja je izgrađena nakon poznate aleksandrijske biblioteke. Pored Kuće Mudrosti, al Mamun je postavio i observatorij u kojem su muslimanski astronomi mogli nastaviti razvijati znanje naslijeđeno od prethodnih generacija. Al Khwarizmi i Banu Musa, takođe matematičar, su bili učenici u bagdadskoj Kući Mudrosti. Dok su studirali i pisali na temu algebre, geometrije i astronomije bili su uključeni i u prevođenje grčkih naučnih rukopisa. Al Khwarizmi je radio pod pokroviteljstvom al Mamuna kojem je posvetio i dva svoja teksta. To su bila njegova studija o algebri i studija o astronomiji. Njegova studija o algebri pod imenom "Hisab al džabr we al muqabala" koje je bila najznačajniji i najvažniji od svih al Khwarizmi-jevih radova počinje riječima:
"Za račun Al Džabra i Al Mukabala sastavio sam ovu konciznu knjigu koja obuhvata istančani i proslavljeni dio računanja. Na to me je ohrabrio Mamun, Knez vjernika, koji budi snagu kod ljudi od obrazovanja, privlači ih, okuplja, štiti, pomaže. On ih podstiče da mutno učine jasnim i složeno prostim."
Na osnovu ovog djela ciivilizacija je dobila novu riječ, “algebra”. Ovo je prva napisana knjiga o ovoj naučnoj disciplini. Važno je shvatiti da je knjiga krajnje praktična i da je algebra uvedena radi riješavanja stvarnih životnih problema koji su bili dio svakodnevnog života u tadašnjoj islamskoj zajednici. Na početku knjige al Khwarizmi opisuje prirodne brojeve na nama danas pomalo neobičan način, ovdje je bitno razumjeti prisutnost potpuno nove dubine apstrakcije i razumjevanja.
"Kada sam generalno razmatrao šta ljudi žele u računaju, našao sam da je to uvijek broj. Takođe sam zapazio da je svaki broj sastavljen od jedinica i da svaki broj može biti podjeljen u jedinice. Šta više, pronašao sam da svaki broj koji se može izraziti u opsegu od 1 do 10, nadmašujući predhodni za jednu jedinicu, naknadno 10 je udvostručen ili utrostručen kao što su i prije bile jedinice, dakle nastaje dvadeset, trideset, itd. do sto, onda se sto udvostruči i utrostruči na isti način kao i jedinice i desetice, do hiljadu.... i tako do najdalje granice numeracije."
Uvodeći prirodne brojeve al Khwarizmi predstavlja glavne teme prvog poglavlja knjige, nazvano rješavanje jednačina. Njegove jednačine su linearne i kvadratne i sastavljene od jedinica, korijena i kvadrata. Tako prema al Khwarizmiju jedinica je broj, korijen predstavlja x, a kvadrat je x2. Međutim, iako ćemo mi radi lakšeg razumjevanja koristiti uobičajenu algebarsku notifikaciju, al Khwarizmijeva matematika je u potpunosti urađena u riječima bez korištenja simbola koji su uvedeni tek u 16-tom vijeku. On je prvi matematičar koji je linearne i kvadratne jednačine sveo na jednu od šest formi:
- kvadrati jednaki korijenima
- kvadrati jednaki brojevima
- korijeni jednaki brojevima
- kvadrati i korijeni jednaki brojevima: npr x2+10x = 39
- kvadrati i brojevi jenaki korijenima: npr. x2+21 = 10x
- korijeni i brojevi jednaki kvadratima: npr. 3x+4 = x2
Svođenje se izvodi koristeći dvije operacije al džabr i al muqabala. “Al džabr” se može prevesti kao "upotpunjavanje" i to je proces uklanjanja negativnih članova iz jednačine. Tako, koristeći al Khwarizmijev primjer, “al-džabr” transformiše x2=40x-4x2 u 5x2=40x. Pojam “al muqabala” može se prevesti kao "uravnoteženje, balansiranje" ii to je proces skraćivanja pozitivnih članova istog stepena kada se oni pojavljuju na obje strane jednačine. Na ovaj način dva izvođenja “al-muqabala” operacije izraz 50+3x+x2=29+10x prelazi u 21+x2=7x gdje jedno izvođenje radi sa brojevima a drugo sa korijenima. Dalje, al Khwarizmi pokazuje kako riješava šest tipova jednačina. On koristi i algebarske i geometrijske metode rješavanja, npr. za riješavanje jednačine x2+10x=39, on je napisao:"Kvadrat i 10 korijena je jednako 39 jedinica. Pitanje za ovaj tip jednačina je slijedeće: koji kvadrat koji se kombinuje sa svojih deset korijena će dati ukupnu sumu 39 ? Način rješavanja ovog tipa jednačine je da se uzme jedna polovina korijena. Sada korijeni u problemu prije nas su 10. Stoga uzimamo 5, koji pomnožen sa samim sobom daje 25, količinu koja se doda na 39 daje 64. Uzimajući kvadratni korijen iz 64 koji je 8, oduzeti od 8 polovinu korijena, 5 ostavljajući 3. Broj tri dakle predstavlja jedan korijen od ovog kvadrata, koji je naravno 9. Broj 9 dakle daje kvadrat.."
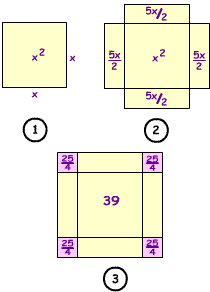
Na gornjoj slici je geometrijsku prikaz zadatka. Al Khwarizmi počinje sa kvadratom strane x, koja dakle predstavlja x2 (slika 1). Kvadratu moramo dodati 10x i ovo je uradjeno dodavanjem četiri kvadrata svaki širine 10/4 i dužine x (slika 2). Površina na prikazana na ovoj slici je x2+10x i iznosi 39. Mi sada kompletiramo kvadrat dodavanjem četiri mala kvadrata svaki područja (5/2)(5/2) = 25/4. Stoga vanjski kvadrat na slici 3 ima podrucje 4(25/4)+39=25+39=64. Iz ovog slijedi da strana kvadrata iznosi 8. Ali strana je od dužine 5/2+x+5/2 tako da je x+5=8, dajući da je x=3. Al-Khwarizmi nastavlja svoju studiju o algebri ispitujući na koji način se zakoni aritmetike proširuju na aritmetiku svojim algebarskim objektima. On tako definira način na koji se mogu izmnožiti izrazi tipa (a+bx)(c+dx). Profesor Rašid vidi nevjerovatnu dubinu i novinu u al Khwarizmi-jevim proračunima kada se isti ispituju iz današnje perspektive. On piše:" ...Skoro da je nemoguće preuveličati originalnost koncepta i stila al Khwarizmi-jeve algebre...", dok Gandž daje sljedeće mišljenje: "Al Khwarizmijeva algebra se smatra kao osnova i kamen temeljac nauka. Potpuno je razumno da se on zove “ocem algebre”, a ne Diophantus, zato što je al Khwarizmi bio prvi u podučavanju algebre u elementarnoj formi i u praktične svrhe dok se Diophantus primarno bavio teorijom brojeva." U nastavku al Khwarizmijeva algebra razmatra praktičnu primjenu i radne primjere. On nastavlja sa traženjem pravila za pronalaženje površina figura kao što je krug i pronalaženje zapremine lopte, kupe i piramide. Ovo poglavlje ima više sličnosti sa indijskim i hebrejskim tekstovima nego sa grčkim radovima. Završni dio knjige se bavi komplikovanim islamskim pravilima naslijednog prava. Al-Khwarizmi je takođe napisao studiju o indijsko-arapskim brojevima. Originalni arapski tekst je izgubljen, a za latinski prevod se zna da je dosta izmjenjen u odnosu na originalni tekst al Khwarizmijevog rada. Ovdje se opisuje indijski brojni system baziran na brojevima 1, 2, 3, 4, 5, 6, 7, 8, 9, i 0 što se danas naziva decimalni brojni sistem. Prvo pravo razumijevanje i primjena nule u brojnom sistemu je vjerovatno posljedica al Khwarizmijevog rada. Razvijene su metode za aritmetičko računanje kao i metoda za pronalaženje kvadratnih korijena za koju se zna da je bila u originalnoj arapskoj verziji premda nedostaje u prijevodu na latinski. Toomer piše:"...decimalni brojni sistem je preuzet od indijskih matematičara...al-Khwarizmijev rad je bio prvi koji ga je sistematski obradio". Drugi važan rad od al Khwarizmija je rad o astronomiji "Sindhind zij" i baziran je na indijskim radovima iz ove oblasti. Indijski tekst na kojem se bazira al Khwarizmijeva studija je predat u bagdadski dvor oko 770. godine kao poklon indijske političke misije. Postojale su dvije verzije al Khwarizmijevog rada napisane na arapskom ali su obje izgubljene. U desetom vijeku al Majriti je napravio reviziju kraće verzije koju je preveo na latinski Adelard of Bath. Postoji i latinska verzija duže verzije i sačuvana su oba ova latniska prijevoda. Glavne teme al Khwarizmijevog rada "Sindhind zij" su kalendari: računanje tačne pozicije sunca, mjeseca i planeta, tabele sinusa i tangensa, sferna astronomija, astroloske tabele, paralaksni i eklipticki proračuni (pomračenje sunca i mjeseca). Al Khwarizmi je napisao i rad iz geografije u kojem se nalaze geografske dužine i širine za 2402 lokacije korištene kao osnova za mapu svijeta. Ova knjiga, koja se bazira na Ptolomejevoj geografiji, nabraja sa gegrafskim dužinama i širinama, gradove, planine, mora, ostrva, geografske regije i rijeke. Rukopis uključuje mape koje su sveukupno preciznije nego Ptolomejeve. O važnosti ovog arapskog matematičara i njegovomi doprinosu svjetskoj civilizaciji dovoljno govore riječi Muhammed Kahna koje ćemo citirati na kraju ove male biografije:
"Na najistaknutijem rangu matematičara za sva vremena stoji al Khwarizmi. On je sastavio najstarije radove o aritmetici i algebri. Oni su bili principijelni izvor matematičkog znanja vjekovima koji su došli na Istok i Zapad. Rad o aritmetici je prvi uveo indijske brojeve u Evropu, dobro poznat kao arapski brojni sistem, rad o algebri je dao ime ovoj važnoj grani matematike u evropskom svijetu..."
