
- Klikova: 17751
"Gausov postupak"
Poznata je anegdota koja kaže da je jednom prilikom Gausov učitelj zadao da se saberu svi brojevi od 1 do 100, vjerovatno da bi "zaposlio učenike". Na njegovo veliko iznenađenje, Gaus (koji je tada imao 7 godina) odmah je donio svoj rezultat: 5050.
- Klikova: 12304
Arbelos - obućarski nož
Arhimed (280 p.n.e - 212 p.n.e), jedan od velikih matematičara, bio je uglavnom zaokupljen problemima iz realnog života i geometrije, mada ovi problemi danas izgledaju više kao rekreativni. Znate li kako je Arhimed izračunao površinu jedne alatke kao što je to obućarski nož ?

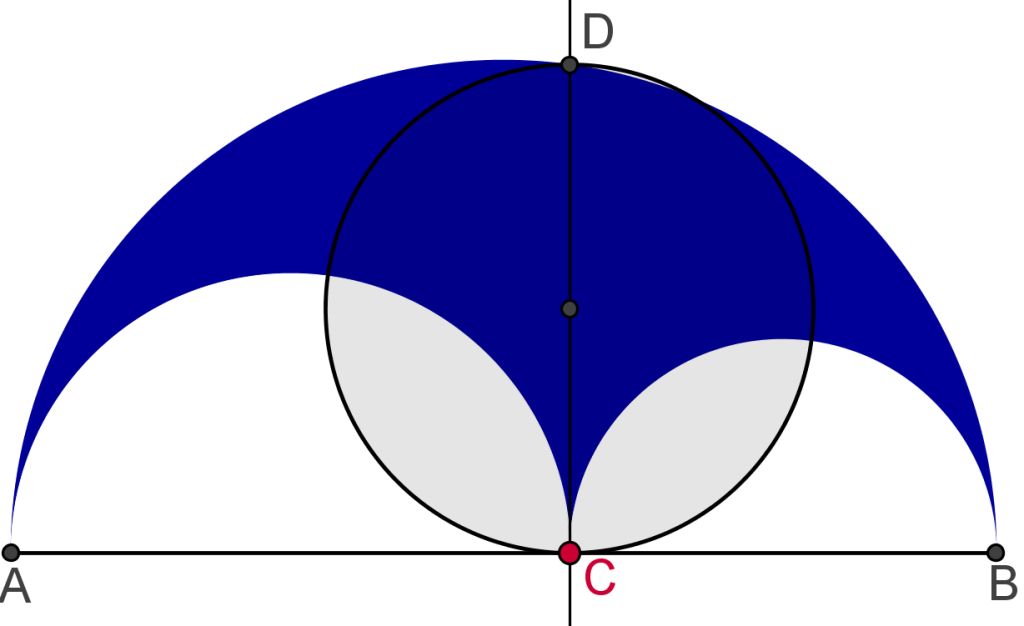
- Klikova: 13921
Poasonov zadatak
 Poznatom francuskom matematičaru Simonu Poasonu u mladosti su postavili jedan logički problem. Pošto se zainsteresovao za problem Poason se oduševio matematikom i posvetio joj cio svoj život. Evo tog zadatka:
Poznatom francuskom matematičaru Simonu Poasonu u mladosti su postavili jedan logički problem. Pošto se zainsteresovao za problem Poason se oduševio matematikom i posvetio joj cio svoj život. Evo tog zadatka:
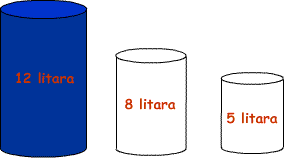
Neko ima 12 litara mlijeka i hoće da pokloni polovinu tog mlijeka svom prijatelju. Međutim, on nema posudu od 6 litara, već jednu od 8 litara, a drugu od 5 litara. Kako može da nalije 6 litara mlijeka u posudu od 8 litara ?  Koliki je najmanji broj prelijevanja pomoću kojih se to može postići ?
Koliki je najmanji broj prelijevanja pomoću kojih se to može postići ?
- Klikova: 17873
Problem četiri boje
Štamparima je poznato da se svaka geografska karta može odštamapati sa četiri boje tako da se dvije zemlje sa zajedničkom granicom oboje različitim bojama.
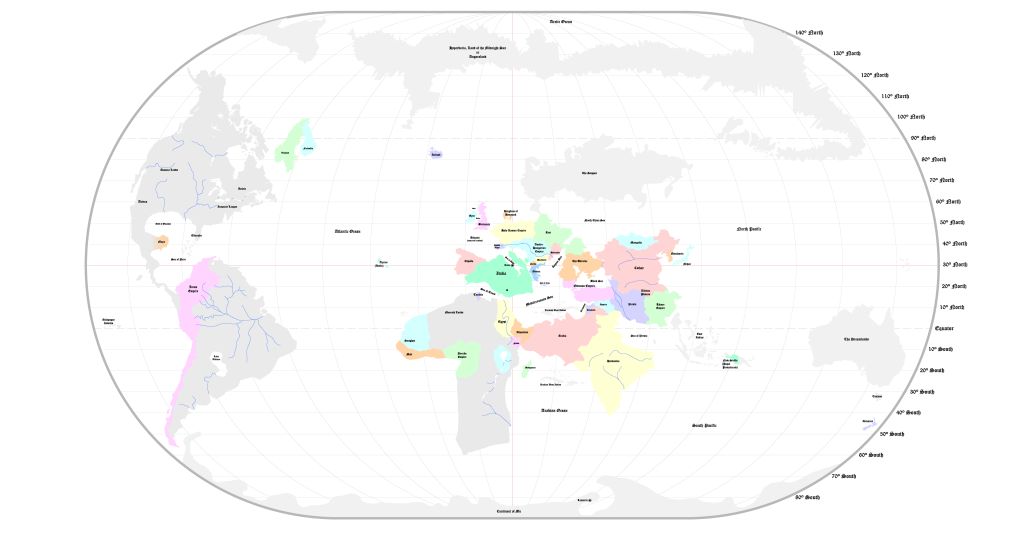
Matematičari de Morgan i Keli postavili su 1850. godine zanimljiv problem:
Može li se svaka geografska karta u ravni
ili na sferi obojiti s najviše četiri boje
tako da zemlje sa zajendničkom granicom
ne budu obojene istom bojom.
Ovaj problem je imao veliki značaj na dalji razvoj teorije grafova. Iako jednostavno forumulisan, on je veoma težak.
- Klikova: 13482
Keningzberški mostovi
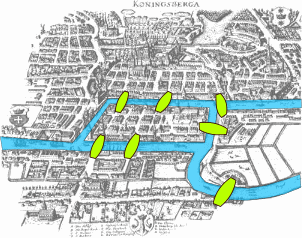 Godine 1736. građani Keningzberga, grada koji je smješten na obalama i ostrvima rijeke Pregel, postavili su pitanje da li je moguće, šetajućii gradom, preći preko svih sedam mostova tako da se nijedan od njih ne pređe više od jednom.
Godine 1736. građani Keningzberga, grada koji je smješten na obalama i ostrvima rijeke Pregel, postavili su pitanje da li je moguće, šetajućii gradom, preći preko svih sedam mostova tako da se nijedan od njih ne pređe više od jednom.