
- Klikova: 14778
Prečnik materijalne lopte

Arapski matematičari su bili zainteresovani za razne konstrukcije na sfernoj površi. Problem određivanja prečnika kugle upotrebom isključivo šestara i lenjira je riješio Tabit ibn Kura (836 - 901).
Zadatak je forumlisan na sljedeći način: "Koristeći Euklidova oruđa (lenjir i šestar) naći prečnik date materijalne lopte."
U nastavku pročitaj na koji način je problem u svoje vrijeme riješio ovaj poznati arapski matematičar.
- Klikova: 4832
Diofantove godine
Postoji više podataka o Diofantovim matematičkim radovima nego o njegovom životu. O nekim detaljima se može saznati preko kolekcije zadataka i zagonetki iz grčke Antologije koju je sastavio Metrodor oko 500. godine naše ere, od koji je sljedeća o Diofantu:
"Diofantovo djetinjstvo trajalo je šestinu njegovog života, oženio se sedminu godina kasnije, brada mu je narasla kada je prošla još dvanaestina, a sin mu se rodio 5 godina kasnije, sin je živio polovinu očevih godina, a otac je umro 4 godine poslije sina. Koliko godina je živio Diofant ?"
- Klikova: 12415
Heronovo najkraće rastojanje
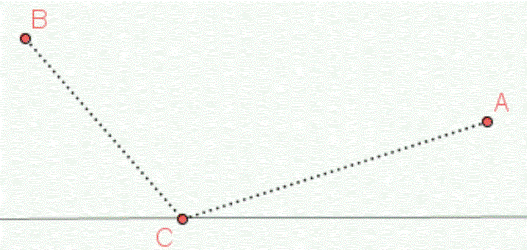
Koristeći jednostavne geometrijske argumente čuveni antički matematičar Heron iz Aleksandrije (oko 65 p.n.e - oko 125 p.n.e) je posmatrao sljedeći problem.
A i B su dvije date tačke sa iste strane prave. Odrediti tačku C na pravoj tako da suma rastojanja od A do C i od C do B bude minimalna.
U praktičnom životu možemo reći da je prava željeznička pruga, dok su tačke A i B gradovi, a tačka C je buduća željeznička stanica koju treba sagraditi. Potrebno je odrediti mjesto gdje će se graditi željeznička stanica tako da je ukupna dužina puteva kojima su gradovi spojeni sa stanicom najkraća.
- Klikova: 11868
Keningzberški mostovi
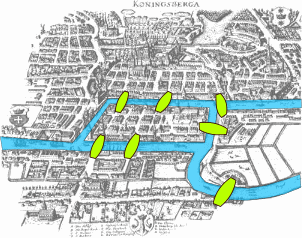 Godine 1736. građani Keningzberga, grada koji je smješten na obalama i ostrvima rijeke Pregel, postavili su pitanje da li je moguće, šetajućii gradom, preći preko svih sedam mostova tako da se nijedan od njih ne pređe više od jednom.
Godine 1736. građani Keningzberga, grada koji je smješten na obalama i ostrvima rijeke Pregel, postavili su pitanje da li je moguće, šetajućii gradom, preći preko svih sedam mostova tako da se nijedan od njih ne pređe više od jednom.
- Klikova: 12978
Ispravna matematika

Dvojica prijatelja su zajedno putovali. Jedan od njih je sa sobom ponio pet pogačica, a drugi je imao samo tri. Na putu im se pridružio stranac koji nije imao hrane, već je dijelio njihove pogačice s njima. Kad su se rastajali, čovjek im je dao osam dirhema kao nagradu za njihove pogačice. Tad se pojavio nesporazum između dvojice prijatelja oko podjele novca. Čovjek, koji je imao pet pogačica je mislio da njemu pripada pet dirhema, a onome koji je imao tri pogačice pripadaju tri dirhema. Drugi je zahtijevao da novac podijele na jednake dijelove tako da svaki od njih dobije po četiri dirhema. Pošto ni jedan nije odustajao od svog stava, obratili su se halifi Aliji sa zahtjevom da im presudi.
- Klikova: 17450
Hijeronova kruna
