Puno ime ovog matematičara inžinjera je Ebu Bekr ibn Muhamed ibn al Husein (ili Hasan u nekim izvorima) al Karađi. Tačnije spominju se dva imana al Karađi i al Karki; Karađ je grad u Iranu i ako je matematičarevo ime al Karađi onda zasigurno njegova familija vodi porijeklo iz ovog grada, dok je Kark predgrađe Bagdada, što navodi na zaključak da ovaj matematičar dolazi iz predgrađa Bagdada.
    
     Istoričari su podjeljeni u tome koja je interpretacija tačna, međutim u tekstovima se danas najčešće navodi al Karađi. Poznato je da je al Karađi veći dio svog života proveo u Bagdadu, i u to vrijeme su i nastali njegovi glavni matematički radovi. Njegova važna studija o algebri, Al Fakhri, je posvećena tadašnjem vladaru Bagdada. Međutim, u jednom momentu svoje karijere on napušta Bagdad i odlazi živjeti u "planinske zemlje". Izgleda da je ovim odlaskom iz grada Al Karađi odustao od matematike i koncentrisao se na inženjerske stvari.

     Doprinos al Karađi-ija u razvoju matematike se različito posmatra od strane raznih autora, baš kao i u slučaju al Khwarizmi-ija; neki autori smatraju da je njegov rad samo prerada radova ranijih matematičara, dok drugi smatraju da je on prva osoba koja je oslobodila algebru od geometrijskih operacija i zamijenila ih sa aritmetičkim operacijama što danas predstavlja osnovu algebre. Woepcke je prvi istoričar koji je uvidio važnost al Karađi-evog rada sa čim su se složili mnogi kasniji autori. On to opisuje kao prvo pojavljivanje:  

   .. teorije algebarskog računanja...

     Takođe i Rashed uočava važnost al Karađi-ija:
 

...manje-više cilj al Karađi-ija je bio da nađe značenje u shvatanju i specifičnosti algebre, da bi se mogla odbaciti geometrijska prezentacija algebarskih operacija...

     Rashed dalje navodi doprinos al Karađi-ija:

...al Karađi-ijev rad zauzima važno mjesto u historiji matematike... otkrivanju i čitanju aritmetičkog rada Diofanta (Diophantus), u svijetlu algebarske koncepcije i metoda al Khwarizmi-ija i drugih arapskih algebrista, praveći nova odstupanja u algebri...


     Koja su to nova odstupanja najbolje opisuje al Samawal, jedan od al Karađi-ijevih nasljednika:

... operisanje sa nepoznatima koristeći aritmetičke alate, na isti način kako aritmetičari operišu sa poznatim.

     Ono što je al Karađi postigao u Al- Fakhri je prvo definisanje monoma
i 
, te postavljanje pravila množenja za bilo koji od ovih monoma, bez bilo kakvog upućivanja na geometriju. Dozvoljavao je i racionalne eksponente. U stvari on skoro da je dao formulu:
 

xⁿx^m=x^m+n za sve cijele brojeve n i m

ali nije uspio da definiše da je x⁰=1...
    
     Kod njega se mogu naći i začeci matematičke indukcije: u dokazu prvo pokazuje tvrdnju za n=1, pa za n=2 pomoću već dokazanog n=1, zatim za n=3 pomoću n=2 i tako do n=5 uz komentar da bi se sa ovim postupkom moglo nastaviti u beskonačnost.
    
     Jedan od rezultata u kojima al Karađi koristi formu indukacije pojavljuje se u njegovom radu o binomnoj teoremi, binomnim koeficijentima i Pascalovom trouglu. U Al-Fakhri al Karađi je izračunao (a+b)³, a u al Badi je izračunao (a-b)³ i (a+b)⁴. Generalna konstrukcija Pascalovog trougla koju je dao al Karađi u svom radu je opisana kasnije u spisima al Samawala:

      Prisjetimo se principa za neophodan broj množenja ovih stepeni jedan sa drugim, za bilo koji broj podjeljen u dva dijela. Al Karađi kaže da se mora postaviti "jedinicu " u tablicu i "jedinicu" ispod prve "jedinice", pomjerajući prvu "jedinicu" u drugu kolonu, dodavajući prvu "jedinicu" ispod prve "jedinice". Tako da se dobije "dvica", koju stavljamo ispod prenesene"jedinice" i stavljamo drugu "jedinicu" ispod "dvice". Dakle mi imamo "jedinicu", "dvicu" i "jedinicu".

     Dalje al Samawal nastavlja da opisuje al Karađi-jev rad, kako druga kolona od brojeva 1, 2, 1 odgovara kvadriranju (a+b):

Ovo pokazuje da svaki broj koji se sastoji od dva broja, i ako svaki pomnožimo sa svakim-budući da su dva ekstrema "jedan" i "jedan"- i ako jedan pomnožimo sa dvostrukim drugim-budući da je srednji član "dva" - dobije se kvadrat ovog broja.

     Ovo je divan opis binomijalne teoreme koristeći Pascal-ov trougao. 
 

    
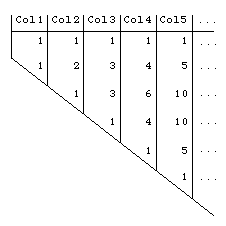
     Drugi rezultati koji je dao al Karađi uključuju zbrajanje prvih n prirodnih brojeva, te kvadrat i kub prvih n prirodnih brojeva. On je dokazao da je suma prvih n prirodnih brojeva jednaka n(n+1)/2.U današnjoj notaciji to izgleda kao:

     Takođe da je

     Al Karađi je pokazao da je (1+2+3+ ...+10)² = 1³+2³+3³+...+10³. On je prvo ovo uradio pokazujući da je (1+2+3+...+10)²=(1+2+3+...+9)²+10³. To isto pravilo mogao je primijeniti na (1+2+3+...+9)², zatim na (1+2+3+...+8)² itd. da se dobije

(1+2+3+ ...+10)²
=(1+2+3+...+8)²+9³+10³
=(1+2+3+...+7)²+8³+9³+10³
...

=1³+2³+3³+...+10³
    
     Na kraju spomenut ćemo uticaj Diofanta na al Karađi-ija. Prvih pet knjiga Diofantove Aritmetika je preveo na arapski ibn Liqa oko 870 godine, a prostudirao ih al Karađi.
     
     Al Karađi je takođe otkrio i mnogo novih problema, dok se problemi koje je naveo Diofant nisu mogli uzeti bez daljeg razvoja. On je uvijek pokušavao da generalizuje Diofantove rezultate i nađe metode koje se primjenjuju na generalne slučajeve.
     
    Al Karađi nije dao doprinos samo u algebri, takođe postoje i njegovi radovi iz geometrije kao što je rad O veličinama za mjerenje građevina i struktura. Al Karađi definiše tačke, linije, površine, čvrsta tijela i uglove. Takođe daje pravila za mjerenje ravnih i čvrstih tijela koristeći lukove, kao i postavljanje metode za mjerenje različitih supstanci.

 Izvor: Math Tutor History