
- Klikova: 13192
Euklid (oko 330-260 p.n.e)
Iako su nam naučni radovi drevnih mislilaca dobro poznati, često su njihovo vrijeme i njihovi životi magloviti, sto sasvim sigurno vrijedi i za Euklida. Premda je njegovo ime poznato svakom srednjoškolcu, o njegovu se životu ne zna gotovo ništa, ni gdje je studirao, pa čak ni gdje se rodio i umro: pravi svjetski misterij!
- Klikova: 11879
Al Kaši (1380 - 1429)

Detalji iz života Ghiyath al Din Džamšfid Mas`ud Al Kašija (1380, Kashan,Iran-22 juni 1429, Samarkand, Transoxania (sada Uzbekistan) su više poznati nego detalji mnogih drugih matematičara tog perioda. Jedan od razloga je i to što je on stavljao tačne datume pisanja svojih radova, a drugi razlog su sačuvana pisma koja je pisao svom ocu.
Al-Kaši je rođen u Kašanu, koji leži u pustinji na istočnom kraju centralne iranske oblasti. Za vrijeme Al Kašijevog odrastanja, Timur je već osvojio velika područja i proglasio se vladarem mongolskog carstva u Samarakandu 1370 godine, a 1383 osvojio je i Perziju sa glavnim gradom Herat. Timur je umro 1405, a njegovo carstvo je bilo podjeljeno između njegova dva sina.
- Klikova: 10506
Edouard Lucas (1842 - 1891)

Francuski matematičar rođen 4. 4. 1842 u Amijenu (Francuska) a umro 3. 10. 1891 godine. Radio je u Pariskoj opservatoriji i kao profesor matematike u Parizu. Poznat je zbog svojih rezultata u teoriji brojeva, posebno je izučavao Fibonačijev niz i njemu pridružen Lucas-ov niz (nazvan po njemu). Lucas je razvio značajne metode za testiranje prostih brojeva, od kojih se poboljšani Lucas-Lemerov test koristi i danas.
- Klikova: 13792
Johan Friedrich Carl Gaus (1777. - 1855.)
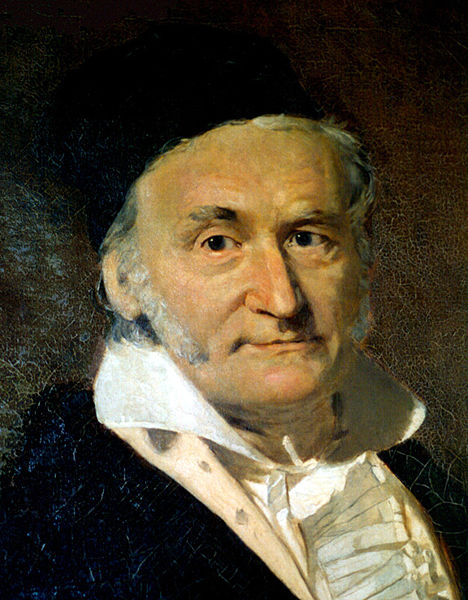
Rođen 30. travnja 1777, godine u Braunschweigu u kolibi kao sin Gerharda i Doroteje. Johan Friedrich Carl Gauss nije imao gotovo nikakvih uvjeta za bavljanje matematikom. Otac mu je bio siromašan čovjek kojeg je plašilo sve što je bilo vezano uz znanost. Srećom, Gaussov ujak pobrinuo se da Carl nastavi školovanje. O genijalnosti malog Carla dovoljno govori kako nije imao ni pune tri godine kada je jednom prilikom napomenuo ocu kako mu izračun nije točan i naravno bio je tada u pravu. Kada je pošao u školu Carl je zapanjio svog surovog učitelja Bütnera koji je obožavao maltretirati djecu. Riješivši njegov najteži zadatak za minutu Gauss je stekao veoma značajnog prijatelja. Bütner, oduševljen, kupio je od svoga novca Carlu matematičke knjige izjavivši da dječak zna više od njega. Međutim u svemu je najsretnija okolnost bila što je u školi kao pomoćni učitelj radio izvjesni Bartels koji je shvatio što se krije u malom Carlu. Zato je poduzeo sve kako bi dječaku osigurao bogatog mecenu. Carl Wilhelm Ferdinand, vojvoda od Braunschweiga primio je dječaka čija skromonost, plašljivost ali prije svega genijalnost očarale.
- Klikova: 10224
Šaraf al Din al Tusi (1135 - 1213)
Puno ime Šaraf al Din al Tusija je Šaraf al Din al Muzaffar ibn Muhammad ibn al Muzaffar al Tusi. O njegovom životu se zna veoma malo, ali se nekoliko detalja može rekonstruisati iz referanci koje se pojavljuju u radovima drugih naučnika tadašnjeg doba. Iz imena se da zaključiti da je rođen u regiji Tus, na sjeveroistoku Irana. Ova regija je uključivala grad Tus i obližnji grad Meshed, visoko u dolini rijeke Kashaf. Ono što je sigurno je da je veći dio života proveo u različitim gradovima. Godine 1154, Seljučki Turci osvajaju Damask u Siriji i čine ga glavnim gradom njihove velike imperije. Grad je napredovao, što je mnoge i privuklo, uključujuči i al Tusija. Oko 1165 godine al Tusi je bio u Damasku, gdje ga je Abu`l Fadl podučavao radovima Euclida i Ptolomeja. Abu`l Fadl je bio interesantna osoba, on je radio kao drvosjeća, stolar prije nego što je al Tusija podučavao matematici. Iz Damaska je al Tusi prešao u Aleppo, drugi najveći grad u Siriji.
- Klikova: 12068
Al Hejsem - Alhazen (965 - 1040)
 Abu Ali al-Hasan ibn Al Hejsem (al Haytham), nadimka al-Basri (po gradu Basri u Iraku) i al-Misri (jer je porijeklom iz Egipta), je uvodeći praksu potvrde hipoteze tek nakon što se ista potvrdi i eksperimentom postavio temelje danas poznatog ,,naučnog metoda" dva stoljeća prije evropskih naučnika. Al Hejsem je najčešće poznat kao Alhazen, što predstavlja latinsku verziju njegovog prvog imena „al-Hasan“; po ovom imenu je nazvan i problem, Alhazenov problem po kojem je al-Haytham pored ostalog i ostao zapamćen:
Abu Ali al-Hasan ibn Al Hejsem (al Haytham), nadimka al-Basri (po gradu Basri u Iraku) i al-Misri (jer je porijeklom iz Egipta), je uvodeći praksu potvrde hipoteze tek nakon što se ista potvrdi i eksperimentom postavio temelje danas poznatog ,,naučnog metoda" dva stoljeća prije evropskih naučnika. Al Hejsem je najčešće poznat kao Alhazen, što predstavlja latinsku verziju njegovog prvog imena „al-Hasan“; po ovom imenu je nazvan i problem, Alhazenov problem po kojem je al-Haytham pored ostalog i ostao zapamćen:Za dati izvor svjetlosti i sferno ogledalo, nađi tačku na ogledalu od koje će se svjetlost reflektovati prema oku posmatrača.